(pq)(pq) => px(pq) qx(pq);12 Let f R → R be defined by setting f ( x) = 1 / q if x = p / q, where p and q are positive integers with no common factor, and f ( x) = 0 otherwise Show that f is integrable over 0, 1 I'm using the Darboux definition of integration, so I want to prove that for any ϵ > 0 there exists a partition P of 0, 1 such that U ( f, P) − L3, x e N}, Q= {x x≤2,x ∈ W} Find (P∪ Q) x (P∩ Q), where W is the set of whole numbers
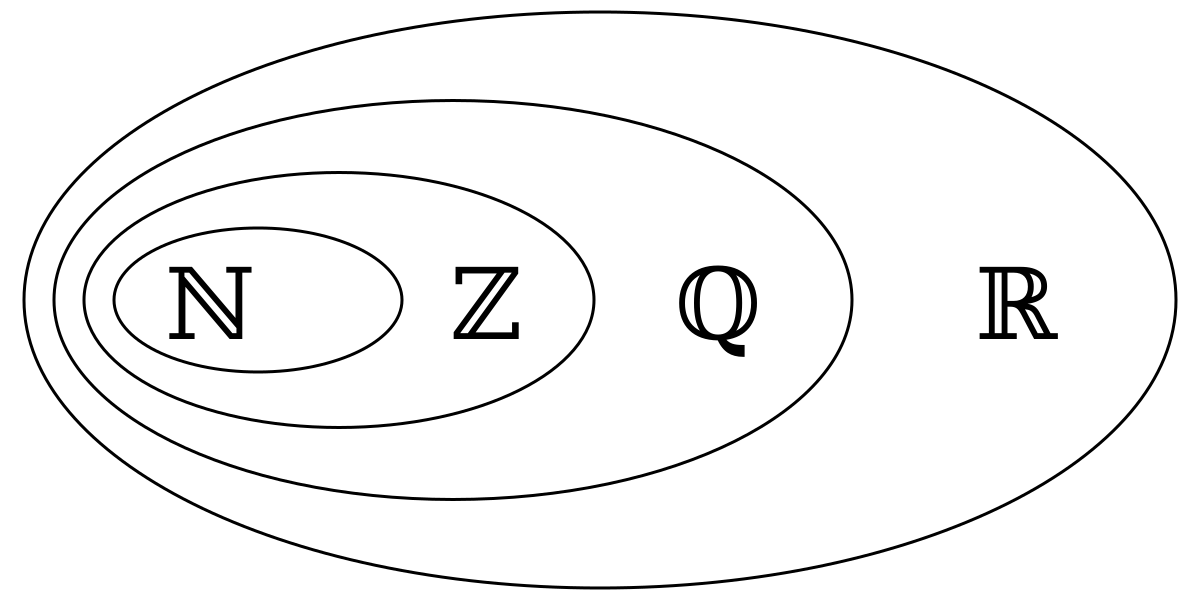
Rational Number Wikipedia
2/8/19 Encuentra una respuesta a tu pregunta xyz=5 xy2z=19 xyz=15 efrain454munoz efrain454munoz Matemáticas Secundaria Xyz=5 xy2z=19 xyz=15 1 Ver respuesta efrain454munoz está esperando tu ayuda Añade tu respuesta y gana puntos oskarsian96 oskarsian96Ejemplo 1 X →N( 8 , 15)Calcula P X < 6 y para terminar y calcular la probabilidad, aplicamos lo que viene a continuación Con esto lo que hemos hecho es simplemente tipificar la variable transformando la probabilidad pedida en una relacionada con la normal N ( 0 , 1 )21/2/ Click here 👆 to get an answer to your question ️ If xyz=3, x^2y^2z^2=5 ,x^3y^3z^3=7,x^4y^4z64=9 then x^5y^5z^5 isnt equal with 1 pleaase quickly
Solve The Given System Of Equations 5 X 4 Y 5 Z Chegg Com
